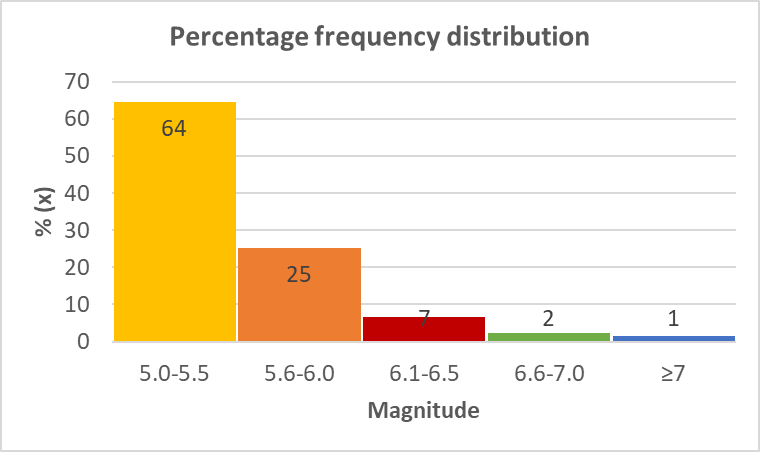
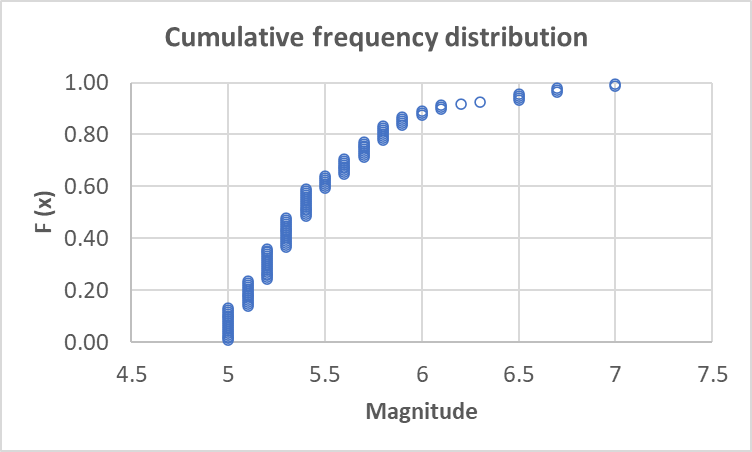
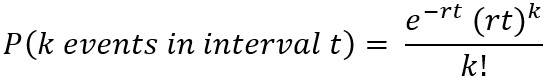Earthquake data analysis: a case study from Italy.

Earthquake data analysis of the seismicity of Italy in the period 1/1/1900 – 25/02/2022 for events with magnitude larger than 5.

General data

INGV provides data on earthquakes that occurred throughout national territory.
We have extracted data of 135 earthquakes of magnitude larger than 5.

Descriptive statistic
Characteristic	Value
Total amount of data	135
Frequency (Total data/Time period)	1.10
Years	123
First data	01 january 1900
Last data	25 february 2022
Maximum	7.0
Minimum	5.0
Position ranking
Mean	5.49
Minimum	5.0
First quartile Q1	5.2
Median	5.4
Third quartile Q3	5.7
Maximum	7.0
Dispersion percentages
Range Q3-Q1	0.5
Range (max-min)	2.0
Standard deviation	0.45
Variance	0.20
Relative variability	0.08

Time relation

The resulting earthquake distribution is investigated in relation to time (periodicities).

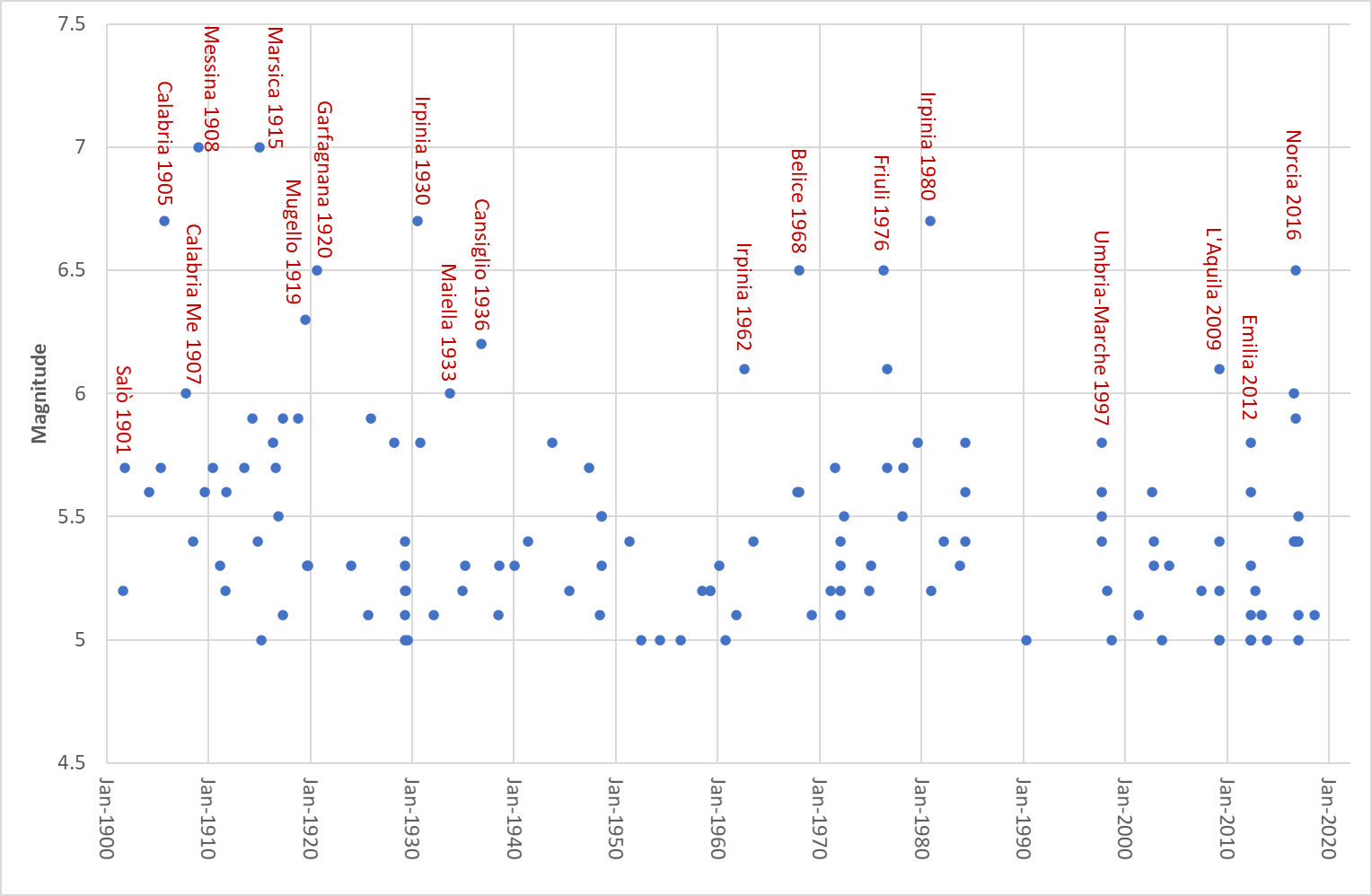
Fig 2.1. Time distribution of seismicity (M 5+) from 1900.

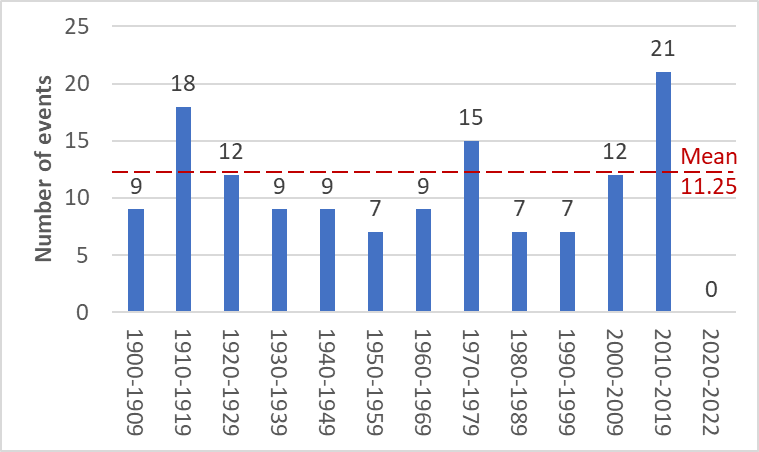
Fig 2.2. Number of events (M 5+) every 10 years.

The greatest number of events occurred in 2010-2019 with 21 (8 events in 2012 and 5 events in 2016);
In 1910-1919 there were 18 events;
In 1970-1979 there were 15 events (5 events in 1972).

Poisson Distribution

The probability mass function (PMF) for the Poisson distribution is:

where k is the number of occurrences, r is the average rate at which events occur, and t is the time interval.
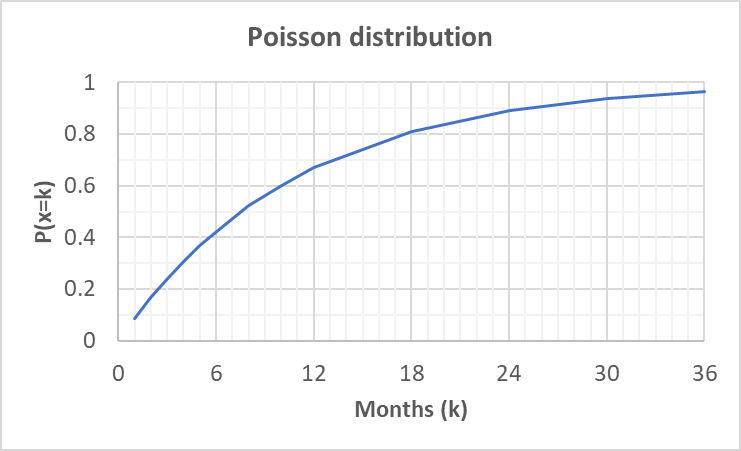
So can we forecast earthquakes using Poisson distribution?

What is the probability that the next earthquake with magnitudo over 5 would hit Italy within 1 month?

First we need to find the rate (r) of the event
135 events in 1465 months (from 1/1/1900 to 25/02/2022). r = 135/1465 ~0.0922
Second we need to find out the probability that an earthquake doesn't occur in a month (t = 1 ; k = 0) and subtract it from 1
p(0)=0.911968188 ; 1-p=0.088031812 ; so it's 8.8%

How about in 12 months? (t = 12 ; k = 0)
p(0)=0.330945342 ; 1-p=0.669054658 ; it's 66.9%

So... can we forecast an earthquake?

Although this way of forecasting has widely been used, it is quite questionable that these probabilities are trustworthy.
Why?
There are 2 big assumption behind the Poisson Distribution:

events must be independent of each other;
the probability of occurrence of an event is constant.

The first assumption is not that true: some earthquakes occur in the same fault line, so they are related to each other.
The second assumption is not true: the probability of occurrence of an earthquake is not necessarily constant.

Data source

[1] E. Guidoboni, G. Ferrari, D. Mariotti, A. Comastri, G. Tarabusi, G. Sgattoni, G. Valensise (2018) - CFTI5Med, Catalogo dei Forti Terremoti in Italia (461 a.C.-1997) e nell’area Mediterranea (760 a.C.-1500). Istituto Nazionale di Geofisica e Vulcanologia (INGV). http://storing.ingv.it/cfti/cfti5/
[2] INGV - Istituto Nazionale di Geofisica e Vulcanologia http://terremoti.ingv.it/